Data Access

Angular Radiation Distribution Model for Earth-Atmosphere System

Shortwave Anisotropic Factor

Standard Deviation of Mean Shortwave Radiances

Correlation of Longwave and Shortwave Radiances

Mean Shortwave Albedo

Day-night Mean Longwave Anisotropic Factor

Standard Deviation of Day-night Longwave Radiances

Daytime Mean Longwave Flux

Day-night Longwave Flux Differences

Readme Contents

Data Set Overview

Sponsor

Original Archive

Future Updates

The Data

Characteristics

Source

The Files

Format

Name and Directory Information

Companion Software

The Science

Theoretical Basis of Data

Processing Sequence and Algorithms

Scientific Potential of Data

Validation of Data

Contacts

Points of Contact

References

Data Set Overview

This readme describes a set of broad spectral band shortwave (0.2 to 4 micron) and longwave (5 to 50 micron) angular radiation distribution models. The satellite measurements of Earth-atmosphere radiations are usually confined to certain local times and specific directions of view depending on orbital constraints and instrument scanning capabilities. However, if angular dependence of reflected and emitted radiation for a surface are known, the total outgoing flux at the top of the atmosphere and the radiations in all directions could be inferred from a single observation (Raschke et al., 1973 ).

Development of angular radiance distribution models has been one of the objectives of the Earth Radiation Budget experiment (ERB) on the Nimbus-7 satellite (Jacobwitz et al., 1984). A comprehensive set of angular radiance distribution models presented here (Suttles et al. 1988a, 1988b ) have been derived primarily from radiances measured between 1978 and 1980 by the Nimbus-7 E RB scanner. In data sparse regions the parameters have been estimated including observations from Geostationary Operational Environmental Satellite (GOES) because of its better diurnal sampling capability ( Minnis and Harrison, 1984 ). The data gaps were filled by variety of other technniques including interpolation and extrapolation based on the reciprocity principle, some empirical and radiative transfer models (Suttles et al. 1988a, 1988b).

The parameters of the shortwave angular radiance distribution model consist of both bidirectional and directional parameters. The bidirectional parameters are anisotropic factor, standard deviation of shortwave (SW) radiances, and shortwave-longwave radiance correlation coefficient as a function of 10 solar zenith angle, 7 viewing zenith angle, 8 relative azimuth angle and 12 scene categories. The directional parameters are mean albedo as a function of solar zenith angle and mean albedo normalised to overhead Sun.

The longwave angular radiance model parameters are anisotropic factor and standard deviation of longwave (LW) radiances as a function of 7 viewing zenith angle, 10 colatitude, 4 season and 12 scene categories. The directional parameters are mean daytime longwave flux and (day - night) longwave flux difference derived as a function of 10 colatitudes and 4 seasons. The longwave daytime flux difference is given only for 10 scene types.

The angular bidirecctional and directional radiation distribution model have been used in the analysis of satellite measurements, earth radiation budget studies and in particular by the Earth Radiation Budget Experiment (ERBE) team in the ERBE inversion algorithm (Barkstrom et al., 1989) as a tool for infering hemispheric fluxes from ERBE radiances (Smith et al., 1986; Wielicki and Green, 1989).

Sponsor
The production and distribution of this data set are funded by NASA's Earth Science enterprise. The Data are not copyrighted; however, we request that when you publish data or results using these data please acknowledge as follows:

The authors wish to thank the following investigators:

• J.T. Suttles, R.N. Green, P. Minnis, G.L. Smith, W.F. Staylor, and B.A. Wielicki
  Langley Research Center, Hampton, Virginia
• I.J. Walker and D.F. Young
  Planning Research Corporation, Hampton, Virginia
• V.R. Taylor and L.L. Stowe
  NOAA National Environmental Satellite, Data and Information Service, Washington, D.C.

for the production of this data set, and the Distributed Active Archive Center (Code 902) at the Goddard Space Flight Center, Greenbelt, MD, 20771, for putting these data in their present format and distributing them. These distribution activities were sponsored by NASA's Earth Science enterprise.

Original Archive
This data sets original archive was at the National Space Sciences Data Center, Goddard Space Flight Center, Greenbelt, Maryland 20771, however it is no longer there.

Future Updates
Revisions of this data are not planned in the near future.

The Data

Characteristics
The angular radiation model consists of eight parameters (listed below), which are surface type based global means and time invariant (measurements are averaged over the period from 1978 to 1980).

Parameters	Units	Range
SW anisotropic factor	unitless	0.410 - 12.764
Standard deviation of SW radiances	W/(m2-sr)	0.383 - 116.40
Correlation of LW and SW radiances	unitless	-0.598 - 0.685
Mean SW albedo	unitless	0.076 - 0.679
Day-night mean LW anisotropic factor	unitless	0.837 - 1.067
Standard deviation of day-night LW radiances	W/(m2-sr)	2.438 - 15.772
Daytime mean LW flux	W/m2	123.61 - 350.54
Day-night LW flux differences	W/m2	-41.67 - 60.04

The Model
The parameters were calculated as a function of 12 scene types.

Scene type	Acronym	Cloud coverage (%)
Clear over ocean	clo	0 - 5
Clear over land	cll	0 - 5
Clear over snow	cls	0 - 5
Clear over desert	cld	0 - 5
Clear over land-ocean mix	clm	0 - 5
Partly cloudy over ocean	pco	5 - 50
Partly cloudy over land or desert	pcl	5 - 50
Partly cloudy over land-ocean mix	pcm	5 - 50
Mostly cloudy over ocean	mco	50 - 95
Mostly cloudy over land or desert	mcl	50 - 95
Mostly cloudy over land-ocean mix	mcm	50 - 95
Overcast	ovr	95 - 100
Day-night LW flux difference divides overcast into overcast over ocean (ovo) and overcast over land (ovl).

Shortwave Angular Model Specifics

For each of the twelve scene types , the SW anisotropic factor, SW Standard deviation and correlation of LW and SW were calculated as a function of:

• 10 solar zenith angles
• 7 viewing zenith angles
• 8 relative azimuth angles

The mean SW albedo were calculated as a function of 10 solar zenith angles, for each of the twelve scene types.

Solar zenith angle, deg.	Viewing zenith angle, deg.	Relative azimuth angle, deg.
0 - 25.84	0 - 15	0 - 9
25.84 - 36.87	15 - 27	9 - 30
36.87 - 45.57	27 - 39	30 - 60
45.57 - 53.13	39 - 51	60 - 90
53.13 - 60.00	51 - 63	90 - 120
60.00 - 66.42	63 - 75	120 - 150
66.42 - 72.54	75 - 90	150 - 171
72.54 - 78.46		171 - 180
78.46 - 84.26
84.26 - 90.00

The relative azimuth angle is measured from the principle plane on the side away from the Sun. The principle plane is defined as the plane containing the ray from the Sun to the target area and the zenith ray that is normal to the target area. Symmetry about the principal plane is assumed for the azimuth angle. Thus, forward reflecting corresponds to 0 degrees and backward reflecting corresponds to 180 degrees azimuth.

Longwave Angular Model Specifics

For each of the twelve scene types, the LW anisotropic factor and LW Standard deviation were derived as a function of:

• four seasons
  • winter northern hemisphere (Dec., Jan., Feb.)
  • spring northern hemisphere (Mar., Apr., May.)
  • summer northern hemisphere (Jun., Jul., Aug.)
  • fall northern hemisphere (Sep., Oct., Nov.)
• 10 colatitude regions
• 7 viewing zenith angles

The LW radiation flux were calculated as a function of four seasons (listed above) and 10 colatitude regions . As usual the LW fluxes are given for each of the twelve scene types. However there are only ten scene types for the (day - night) flux difference parameter. The combined land/ocean scenes are not present while the overcast scene is divided into overcast over land and overcast over ocean.

Colatitude angle, deg.	Viewing zenith angle, deg.
0 - 18	0 - 15
18 - 36	15 - 27
36 - 54	27 - 39
54 - 72	39 - 51
72 - 90	51 - 63
90 - 108	63 - 75
108 - 126	75 - 90
126 - 144
144 - 162
162 - 180

Source
The angular radiation models were derived primarily from Nimbus-7 Earth Radiation Budget (ERB) radiance measurements (Jacobowitz et al. 1984). Cloud data came from the Nimbus-7 Cloud Climatology (Stowe et al., 1988) which was developed from the measurements from two additional Nimbus-7 instruments, the Temperature and Humidity Infrared Radiometer (THIR) and the Total Ozone Mapping Spectrometer (TOMS). The radiance and cloud measurements were combined and the anisotropic SW and LW factors derived by the procedure described in Taylor and Stowe (1984 & 1986). Because the Nimbus-7 satellite was in a Sun-synchronous orbit, no data was obtained for a number of the angular bins. Suttles et al. (1988 & 1989) describe how these bins were filled in. In particular a number of the directional albedos were derived from Geostationary Operational Environmental Satellite (GOES) measurements. For the GOES results, the analysis of November 1978 GOES-East data by Minnis and Harrison (1984b, 1984c) was used.

Specifications for the ERB scanner are:

• noon Sun-synchronous orbit
• scanner consists of four optical telescopes
• each telescope has the following broadband channels:
  • shortwave (0.2 to 4 microns)
  • longwave (5 to 50 microns)
• multiaxis scanning capability:
  • scans from horizon to horizon along the orbital track
  • scans to a viewing zenith angle of 72 degrees in the cross-track direction
• spatial resolution:
  • 90 km x 90 km at nadir
  • 250 km x 250 km at the maximum scan angle.

A more detailed description of the ERB instrument exists in Jacobowitz et al. (1984).

The Files

Format

Data Files

• File Size: range in size from 204 to 3430 bytes
• Data Format: ascii text
• Headers, trailers, and delimiters: see file organization
• Fill value: -99.99
• File organization:
  • Each of the SW anisotropic, SW standard deviation and SW-LW correlation coefficient files contain data from a specific scene type. The files contain 10 blocks of 8 rows, each block being measurements from a specific solar zenith angle range. First row of each block is a header indicating the solar zenith angle and the next 7 rows contain parameter values as a function of relative azimuth angles (8 columns) and viewing zenith angles (7 rows).

  • The mean SW albedo (directional parameter) has very simple file structure compared to bidirectional parameter. There is no header in the data file. Data is represented in a matrix as function of scene type (12 rows) and solar zenith angle (10 column).

  • Each of the LW anisotropic and LW standard deviation files contain data from a specific scene type. The files contain 4 block of measurements representing the specific season, starting with the winter and ending with fall. In each block the header indicates the season, and the parameter values are presented as a function view zenith angles (7 rows) and colatitude angles (10 column)

  • The daytime LW flux and day-night LW flux difference files contain 12 and 10 blocks, respectively. Each block represents data for a specific scene type starting with a scene header and then the parameter values follow as function of season (4 rows) and colatitude angles (10 column).

NAME AND DIRECTORY INFORMATION

Naming Convention

The file naming convention for the angular radiation model dataset is

erbe_ang.pppppp.sss.asc and

erbe_ang.pppppp.asc

where:

erbe_ang = data product designator (angular radiation models)

pppppp = parameter designator

swanis = shortwave anisotropic factor

swstdv = standard deviation of shortwave radiances

swcorr = correlation of LW and SW radiances

swalbd = shortwave albedo

lwanis = longwave anisotropic factor

lwstdv = standard deviation of longwave radiances

lwflux = longwave radiation flux

lwfldn = day-night longwave radiation flux difference

sss = scene type designator

clo = clear over ocean

cll = clear over land

cls = clear over snow

cld = clear over desert

clm = clear over land-ocean mix

pco = partly cloudy over ocean

pcl = partly cloudy over land

pcm = partly cloudy over land-ocean mix

mco = mostly cloudy over ocean

mcl = mostly cloudy over land

mcm = mostly cloudy over land-ocean mix

ovr = overcast

asc = file type designator (ascii)

Plots of the angular radiation models data set have been provided in gif format. The file naming convention for these files are

erbe_ang.pppppp.sss.gif and

erbe_ang.pppppp.sss.aaaaaa.gif

where:

erbe_ang = data product designator (as listed above)

pppppp = parameter designator (as listed above)

sss = scene type designator (as listed above), with the addition of land, ocean and snow (snow and desert) designators for the SW albedo gifs

aaaaaa = azimuth designator

0 - 26 = 0 - 25.84 degrees

26 - 37 = 25.84 - 36.87 degrees

37 - 46 = 36.87 - 45.57 degrees

46 - 53 = 45.57 - 53.13 degrees

53 - 60 = 53.13 - 60.00 degrees

60 - 66 = 60.00 - 66.42 degrees

66 - 72 = 66.42 - 72.54 degrees

72 - 78 = 72.54 - 78.46 degrees

78 - 84 = 78.46 - 84.26 degrees

84 - 90 = 84.26 - 90.00 degrees

gif = file type designator (Graphics Interchange Format)

Directory Path to ASCII Files and Image Files

/data/inter_disc/remote_sensing_science/erbe_angle/pppppp

where pppppp are:

swanis = shortwave anisotropic factor directory

swstdv = standard deviation of shortwave radiances directory

swcorr = correlation of LW and SW radiances directory

swalbd = shortwave albedo directory

lwanis = longwave anisotropic factor directory

lwstdv = standard deviation of longwave radiances directory

lwflux = Daytime mean longwave radiation flux directory

Companion Software

Since the data files are in Ascii format, no formal read program is provided.

The Science

Theoretical Basis of Data
Analysis of satellite measurements for determination of the Earth's radiation budget requires information about the angular characteristics of radiation that is reflected (shortwave) and emitted (longwave) from the earth-atmosphere system (Smith et al. 1986). The angular radiation model accomplishes this by defining for an imaginary surface at the top of the atmosphere, the exiting radiance for each direction out to space as a function of the total hemispheric flux leaving the element. In principle, a radiance measurement at a single angle can then be converted into an inferred hemispheric flux (Suttles et al., 1988a, 1988b; Wielicki and Green, 1989).

The bidirectional model parameters are based on the relationship between radiance L and flux M. For shortwave model this relationship is the following:

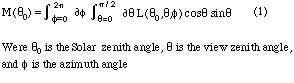
The longwave model relationship is:

An anisotropic function R can be calculated for shortwave where

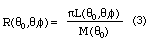
The equation for the longwave anisotropic function R is

The anisotropic function for both the shortwave and longwave are defined as the ratio of the equivalent lambertian flux to the actual flux. Thus, if the surface is lambertian, that is, independent of viewing angles, then R = 1.

The angular radiance model are derived for 12 scene classifications, taking into consideration variations in the reflectivity of different surfaces. The 12 scene type are based on broad categories of climatologically important surface and cloud features and were originally developed for the ERBE data analysis (Smith et al. 1986).

• Surface types of land, desert or ocean were determined a priori by reference to a geographic map or atlas. The desert scene includes vegetated and nonvegetated types.

• Mixed scene types (i.e. clear over land-ocean mix, partly cloudy over land-ocean mix and mostly cloudy over land-ocean mix) were calculated using the assumption that observations of mixed scene are either ocean or land with and equal (i.e. 50-percent) probability of being one or the other (Suttles et al.,1988a, 1988b).

• Snow cover scenes, which include snow and ice, were determine using time-varying snow maps (Fye 1978; Morse and Ropelewski 1983).

• Cloud scene identification, for the bidirectional parameters and LW fluxes, were performed using an improved Nimbus-7 cloud-detection algorithm described by Stowe et al. (1988). This improved algorithm is based on a surface temperature analysis from 3-hourly, Air Force 3-D nephanalysis data (Fye 1978); on reflectance data from the ultraviolet channel of the TOMS; and on infrared window channel emission from the THIR. The cloud analysis for the angular model were performed over the period of April 1, 1979 to June 22, 1980.

• Cloud scene identification for the mean SW albedo was based on an analysis of GOES data using the method of Minnis and Harrison (1984a), which uses 8-km infrared data and 1-km visible data sampled every 8 km.

• Overcast scenes were computed using a weighted average of the overcast-over-ocean and overcast-over-land (Suttles et al., 1988a, 1988b).

Processing Sequence and Algorithms
ERB data were binned according to solar zenith angle, view zenith angle, relative azimuth and scene type for the shortwave bidirectional model, and binned according to view zenith, colatitude and scene type for the longwave bidirectional model. When fewer than eight samples were available for a bin, the mean value for the bin was counted as missing. The following interpolation steps were used for bins that were classified as missing.

Shortwave

• Where values were missing for an entire solar-zenith-angle bin the Helmholtz Principle of Reciprocity (Chandrasekhar 1960) was used, and an empirical relation for desert scenes ( Staylor and Suttles 1986) was used for desert scenes.
• Where values were missing for occasional, isolated viewing-angle bins (which generally occurred at the largest viewing-angle bins) bilinear interpolation was used in most cases. The interpolations was first done along the azimuthal direction and then along the viewing zenith direction. The results from both interpolations are then averaged to get the estimated value. The interpolation schemes used are as follows:
  

  Case	Bin configuration	Interpolated value of x
  1	a x	a
  2	a o x	a
  3	a o o x	Unknown
  4	a x o o	a
  5	a o x o	a
  6	a x b	a/2 + b/2
  7	a x o b	2a/3 + b/3
  8	a x o o b	a
  9	a o x o b	Unknown*
  where "a" and "b" are known values, "o" is an unknown value, and "x" is the value to be determined. *Use x-value in other direction if available; if not available use x = (a/2) + (b/2)

  Case 3 demonstrates an instance in which a value for "x" cannot be determined. In such cases the values are estimated using linear extrapolation or scaling from data in neighboring solar-zenith-angle bins.
• In cases where interpolation produced unusual variations or unreasonable reciprocity results, more reasonable values were estimated.
• After obtaining values for all angle bins, the models were checked using the normalization criterion described in Suttles et al. (1988a). Final model values satisfy the normalization criterion to within + or - 0.0001.

Longwave

• Where missing data occurred for an entire season or colatitude bin, the bin-mean values for all viewing-angle bins were replicated from the seasons or colatitude bins.
• Where bin-mean values were missing for occasional and isolated viewing-angle bins, values were determined by interpolation, extrapolations, or averaging using surrounding viewing-angle bin values. Depending on appropriateness, missing data were filled using one of the following methods:
  1. Replication of data from appropriate season of opposite hemisphere (e.g. Southern Hemisphere winter for Northern Hemisphere winter)
  2. Replication of data from contiguous season of same hemisphere
  3. Replication of data from adjacent colatitude bin
  4. Replication of data from a similar scene type
  5. Replication of data from daytime to nighttime or vice versa
  6. Interpolation, extrapolation, or averaging using values in surrounding bins

Shortwave Directional Model
The mean albedo was derived from a combination of ERB and GOES measurements. The directional models are normalized by dividing each bin value of albedo by the value for the first solar-zenith-angle bin. Thus, the model can be defined in terms of the normalized function (a shape function) and the albedo for the first solar bin (a reference value). The GOES yielded the best estimate of the shape function for tropical and subtropical latitudes. The ERB data best described the shape function (except for the lowest solar zenith angles) for middle and high latitudes. A simple average of the GOES and ERB models was used to produce global mean albedos.

Exceptions to this averaging process were:

• In cases of unreasonable changes in albedo, for the ERB data, due to Sun angle (i.e. low albedos for overcast and mostly cloudy scenes over ocean at low solar zenith angles, and mostly cloudy scenes over land at high solar zenith angles) the data was smoothed before being averaged with the GOES data.
• Theoretical results were derived for the shape function, in cases of clear over snow and clear over desert scenes where GOES results were not available and ERB albedos varied greatly in relation to Sun angle. The radiative transfer code for the theoretical calculations is described by Wiscombe et al. (1984).

Scientific Potential of Data
The angular radiation models show the variation of reflective SW and emitted LW radiation, at the top of the atmosphere, due to differences in scene type, viewing zenith angle, solar zenith angle (SW) and colatitude (LW). The results from these models are useful in the study of the anisotropic characteristics of SW and LW radiation and as a source of angular radiance distribution information in the processing of derivative products.

The ERB team used this data set in a combined scene identification and flux estimation algorithm (Wielicki and Green, 1989). The Data set was created in terms of quantized bins, however to produce smoother ERBE products, interpolation curves were fitted through The Data points to produce continuous angular results. In the LW limb darkening tables they also interpolated to obtain continuous latitudinal functions.

Others have also used these models to estimate fluxes from scanner radiance measurements. The original Nimbus-7 ERB scanner flux estimates were made using earlier and cruder algorithms and models. After the construction of the ERB ADMs, the Nimbus-7 ERB scanner fluxes were recomputed using the ERBE algorithm and ADMs (Kyle et al., 1990; Ardanuy et al., 1990). In addition Stowe et al. (1994), Cess et al. (1995), and Hucek and Jacobowitz (1995) used the ADMs in their procedures to estimate broad band fluxes and albedos from narrow spectral band GOES and AVHRR radiance measurements.

There are several points that a user of this data set should keep in mind.

• These are top of the atmosphere results which combine both the surface and atmosphere effects.
• They were developed from broad spectral band measurement and therefore should be applied with some caution to narrow spectral band radiances.
• They are large scale mean results and may not apply well to certain specific scenes. The standard deviations give some indication of the variability of the various scene types.

Validation of Data
The angular models have gone through extensive reviews, with the results described in Suttles et al. (1988a, 1988b). We have also produced gif plots of this data which can be used to easily examine the angular model. The gif files are available on this FTP site.

Contacts

Points of Contact

For information about or assistance in using any DAAC data, please contact

EOS Distributed Active Archive Center (DAAC)

Code 902.2

NASA Goddard Space Flight Center

Greenbelt, Maryland 20771

Internet: daacuso@daac.gsfc.nasa.gov

301-614-5224 (voice)

301-614-5268 (fax)

References

Ardanuy, P. E., C. R. Kondragunta, and H. L. Kyle, 1990: Low- Frequency modes of the tropical radiation budget, Meteorol. Atmos. Phys. , 44, 167-194.

Barkstrom, B. R., E. Harrison, G. Smith, R. Green, J. Kibler, R. Cess, and the ERBE Science Team, 1989: Earth Radiation Budget Experiment (ERBE) archival and April 1985 results, Bull. Amer. Meteor. Soc. , 70, 1254-1262.

Cess, R. C., M. H. Zhang, P. Minnis, L. Corsetti, E.G. Dutton, B. W. Forgan, D. P. Garber, W. L. Gates, J. J. Hack, E. F. Harrison, X. Jing, J. R. Kiehl, C. N. Long, J.-j. Morcrette, G. L. Potter, V. Ramanathan, B. Subasilar, C. H. Whitlock, D. F. Young, and Y. Zhou, 1995: Absorption of solar radiation by clouds: observations versus models, Science, 267, 496-499.

Chandrasekhar, S. 1960. Radiative Transfer. Dover Publ., Inc..

Fye, F. K. 1978. The AFGWC Automated Cloud Analysis Model. AFGWC-TM-78-002, U.S. Air Force, June. (Available from DTIC as AD A057 176.)

Hucek, R., and H. Jacobowitz, 1995: Impact of scene dependence on AVHRR albedo models, J. Atmos. Oceanic Technol. , 12, 697-711.

Jacobowitz, H., H. Soule, L.H. Kyle, House F.B. 1984. The Earth Radiation Budget (ERB) Experiment: An Overview. J. Geophys. Res.., 89(D4):993-1011.

Kyle, H. L., T. R. Hucek, B. Groveman, and R. Frey, 1990: User's Guide: Nimbus-7 Earth Radiation Budget narrow-field-of-view products, NASA Ref. Publ. RP-1246, 76 pp.

Minnis, P. and Harrison, E. F. 1984a. Diurnal Variability of regional Cloud and Clear-Sky Radiative Parameters Derived From GOES Data. Part I: Analysis Method. J. Climate & Appl. Meteorol., 23(7):993-1011.

Minnis, P. and Harrison, E. F. 1984b. Diurnal Variability of regional Cloud and Clear-Sky Radiative Parameters Derived From GOES Data. Part II: November 1978 Cloud Distributions. J. Climate & Appl. Meteorol.., 23(7):1012-1031.

Minnis, P. and Harrison, E. F. 1984c. Diurnal Variability of regional Cloud and Clear-Sky Radiative Parameters Derived From GOES Data. Part III: November 1978 Radiative Parameters. J. Climate & Appl. Meteorol., 23(7):1032-1051.

Morse, Burt J. and Ropelewski, C. F. 1983. Spatial and Temporal Distribution of Northern Hemisphere Snow Cover. NOAA Tech. Rep. NESDIS 6, U.S. Dep. of Commerce, Oct. (Available from NTIS as PB84 118 348.)

Raschke, E., V. Haar, H. Thomas, W. R. Bandeen, M. Pasternak. 1973: The Annual Radiation Balance of the Earth-Atmosphere System During 1969-70 From Nimbus-3 Measurements. J. Atmos. Sci., 30(3): 341-364.

Smith, G. L., R.N. Green, E. Raschke, L.M. Avis, J.T. Suttles, B.A. Wielicki, and R Davis. 1986. Inversion Methods for Satellite Studies of the Earth's Radiative Budget: Development of Algorithms for the ERBE Mission. Review Geophys., 24(2):407-421.

Staylor, F.W. and Suttles J. T. 1986. Reflection and Emission Models for Deserts Derived From Nimbus-7 ERB Scanner Measurements. J. Climate & Appl. Meteorol., 25(2):196-202

Stowe, L.L., C.G. Wellemeyer, T.F. Eck, Y.Y.M. Yeh, and Nimbus-7 Cloud Data Processing Ream. 1988. Nimbus-7 Global Cloud Climatology. Part I: Algorithms and Validation. J. Climate, 1(5):445-470.

Stowe, L., R. Hucek, P. Ardanuy, and R. Joyce, 1994: Evaluating the design of an Earth radiation budget instrument with system simulations. Part II: Minimization of instantaneous sampling errors for CERES-I, J. Atmos. Oceanic Tecnol. , 11, 1169-1183.

Suttles, J.T., R.N. Green, P. Minnis, G.L. Smith, W.F. Staylor, B.A. Wielicki, I.J. Walker, D.F. Young, V.R. Taylor, and L.L. Stowe. 1988a. Angular Radiation Models for Earth-Atmosphere systems. Volume I-Shortwave Radiation. NASA RP-1184, Vol. I.

Suttles, J.T., R.N. Green, G.L. Smith, B.A. Wielicki, I.J. Walker, V.R. Taylor, and L.L. Stowe. 1988b. Angular Radiation Models for Earth- Atmosphere systems. Volume II-Longwave Radiation. NASA RP-1184, Vol. II.

Taylor, R.V. and Stowe, L.L. 1984. Reflectance Characteristics of Uniform Earth and Cloud Surface Derived From Nimbus-7 ERB. J. Geophys. Res., 89(D4):4987-4996.

Taylor, R.V. and Stowe, L.L. 1986. Revised and Emission Models From Nimbus-7 ERB Data. Sixth Conference on Atmospheric Radiation., American Meteorological Soc., pp. J19-J22.

Wielicki, B. A., and R. N. Green, 1989: Cloud identification for ERBE radiative flux retrieval, J. Appl. Meteor. , 28, 1131-1146.

Wiscombe, W.J., R.M. Welch, and W.D. Hall. 1984. The Effects of Very Large Drops on Cloud Absorption: I. Parcel Models. J. Atmos. Sci. 41(8):1336-1355.

NASA	Goddard	GDAAC	CIDC